Covid-19: ¿Qué significa un crecimiento exponencial?

Por Victoria Vampa*. Foto Daniela Amdan. 

A lo largo de la historia la humanidad ha vivido en forma reiterada la aparición de enfermedades que se extienden de manera incontrolada y dejan huellas imborrables en la comunidad, como la peste bubónica, la malaria o la viruela. Actualmente, y gracias al trabajo de equipos multidisciplinarios que incluyen médicos, virólogos, biólogos, matemáticos, físicos, bioingenieros, entre otros, es posible diseñar y organizar respuestas sanitarias apropiadas. Una de las herramientas fundamentales para este objetivo son los modelos matemáticos que permiten formalizar un fenómeno en lenguaje propio de esta disciplina y formular indicadores fiables para evaluar su evolución en el tiempo.

¿Qué significa un crecimiento exponencial?

Los contagios en el marco de las epidemias tienen como propiedad su carácter multiplicativo, es decir que su crecimiento durante una unidad de tiempo es proporcional al número de enfermos. En el caso más sencillo, cada día la cantidad de infectados se multiplica por un cierto factor k mayor que uno. Por ejemplo, para k=2, la cantidad de enfermos sigue una progresión geométrica de razón 2 (ver TABLA 1):

Esto conduce a un crecimiento vertiginoso de la cantidad de infectados en un tiempo muy breve, que responde a lo que en matemática se conoce como función exponencial: para cada día n, la cantidad de enfermos es f(n) = 2n. Los gráficos de este tipo de situaciones pueden verse aquí.

¿Cómo puede medirse la velocidad del crecimiento exponencial?

Una de las formas para cuantificar el crecimiento exponencial consiste en considerar el tiempo que debe transcurrir para que el número de casos ascienda al doble. Si se toma en cuenta la tabla anterior, el tiempo de duplicación es de un día, y a lo largo de D días hay D duplicaciones.

Si en lugar de k=2, consideramos k=4, la cantidad de enfermos se multiplica por 4 cada día (ver TABLA 2):

Y el tiempo de duplicación es medio ½ día, ya que se observa una duplicación 2 veces por día. Por ejemplo, el día 2, duplica 2 veces los enfermos del día 1 (esto da 16; es decir 16=2.2.4).

En tales circunstancias, estamos considerando que un enfermo contagia cada día, a otros 2 o a otros 4. En el caso del coronavirus se ha estudiado que la cantidad que contagia cada infectado está entre 2 y 3, así que correspondería a valores intermedios entre las 2 tablas anteriores.

¿Cómo afecta el aislamiento al tiempo de duplicación? 

Volviendo al primer caso (k=2) de la TABLA 1, supongamos que el día 1 había 2 infectados, pero por el aislamiento solamente uno contagia, y entonces el día 2 sigue habiendo 2 enfermos. Así, por cumplimiento del confinamiento social, en los días 3, 4 y 5 hay 4 infectados, y recién al sexto día hay 6 enfermos porque uno de los 4 infectados no cumplió el aislamiento y contagió a otros 2. Se tendría lo siguiente:

De acuerdo a la tabla el tiempo de duplicación empezó siendo 1 día, luego 2 días (al tercer día hubo 4 casos) y luego 3 días, ya que recién al séptimo día se duplicaron los 4 casos del tercer día. Lo notable es que la cantidad de infectados totales al día 7 sea de 8 en lugar de 27=128. De la comparación entre las tablas 1 y 3 se desprende la beneficiosa desaceleración producida por medidas tales como el aislamiento y el distanciamiento social. 

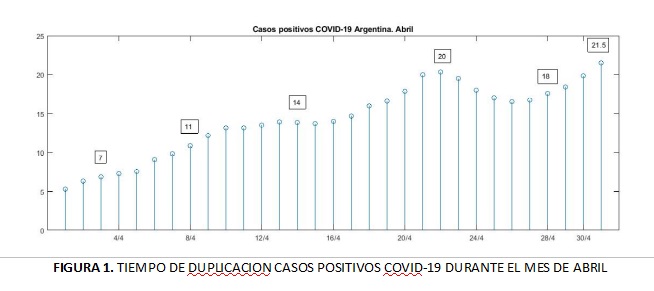
Si bien las epidemias reales son más complejas y no siguen secuencias geométricas como las anteriores, es posible definir un tiempo de duplicación, para cada día, que estime esa velocidad, y nos brinde así información de la evolución de la epidemia en el tiempo. En la Figura 1 que sigue se muestran las estimaciones de los períodos de duplicación de casos positivos de COVID-19 en la Argentina durante el mes de abril. Lo primero que surge es una desaceleración del crecimiento exponencial, ya que el tiempo de duplicación aumentó más de 4 veces, pasando de 5 días a 21.5 días.

Hablamos de estimaciones porque no es posible hallar los tiempos de duplicación en forma exacta. Lo factible es obtener valores aproximados mediante el desarrollo de una técnica y de un programa computacional. Este algoritmo –que no es posible describir con detalle aquí- consiste en ajustar los datos de infectados que brinda diariamente el Ministerio de Salud con una curva exponencial segmentada cada 8 días. Luego, con esos parámetros aproximados y mediante el uso de propiedades matemáticas de la función exponencial, se obtiene, para cada día, la estimación de los días de duplicación.

¿Cómo se modeliza una epidemia?

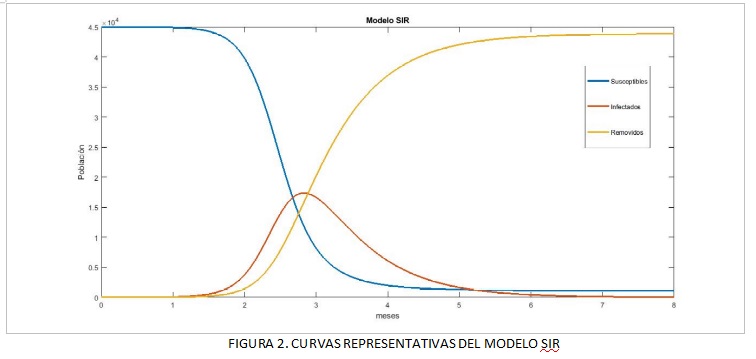
Un punto de partida adecuado para analizar la propagación de epidemias es la adopción del llamado modelo SIR (iniciales de “Susceptibles, Infectados y Recuperados o Removidos”), formulado en 1927, a partir de estudios sobre la malaria, por el médico militar Anderson Gray Mc Kendrick (1876-1943) y el químico William Kermack (1898-1970). En este modelo, la población en la que se desarrolla la epidemia se divide en 3 grupos: 1) los individuos susceptibles de contraer la enfermedad, cuya población representamos por S, 2) los infectados, I y los removidos (que incluyen tanto a los que superan la enfermedad como a los que fallecen por su causa), representados por R. Ver Figura 2. 

Las relaciones entre las cantidades de miembros de cada población, S, I y R en cada tiempo t, responden a tres ecuaciones diferenciales. Así la cantidad de infectados aumenta por ejemplo por el contacto entre susceptibles e infectados y disminuye al crecer los removidos. Además, cabe señalar que una de las suposiciones del modelo es que las suma de los tres grupos es siempre N, que es la cantidad total de la población (S+I+R=N). El estudio de este modelo permitió identificar un parámetro, que suele anotarse R0 que es de gran ayuda para estimar la incidencia de una epidemia, ya que representa el número medio de casos originados por el contagio de un solo infectado al comienzo de la expansión de la enfermedad. Tiene un alto valor predictivo, ya que por debajo del valor crítico R0=1, la epidemia se encuentra en retirada, pero si R0 está por encima de 1, significa que la enfermedad se está extendiendo. Para el caso del COVID-19, hay estimaciones que dieron a R0 un valor aproximado de 2.24. Hay además en el modelo otros dos parámetros importantes que son la tasa de transmisión (que depende de los contactos que tiene cada individuo y de la probabilidad de contagiar a un susceptible) y la tasa de recuperación (que tiene que ver con la duración de la enfermedad). 

¿Los modelos permiten predecir la evolución?

En primer lugar, corresponde aclarar que los modelos matemáticos que se utilizan actualmente son muy distintos del SIR original. Son modelos de epidemia de última generación con más variables y más poblaciones. Incluyen la población de Expuestos, (MODELO SEIR), donde E son los portadores en período de incubación pero asintomáticos, y también a los habitantes en cuarentena, a los pacientes hospitalizados y a los internados en unidades de cuidado intensivos. A veces se agregan estratificaciones por edad, ya que enfermedades como el COVID-19 afecta en forma diferente a jóvenes y a adultos mayores. Otras veces se contemplan parámetros que miden el comportamiento social (recurriendo por ejemplo a las localizaciones que pueden determinarse a través de los teléfonos móviles) u otros parámetros epidemiológicos.

Así, los modelos resultan más complejos, tanto para su tratamiento teórico como para la implementación computacional. Y permiten así mismo realizar predicciones para algunos días siguientes acompañadas de lo que se llama “intervalo de confianza”, que es el rango donde se estima que se ubicarán los valores reales de las variables cuya evolución se busca anticipar.

¿Con las medidas adoptadas se está aplanando la curva de infectados?

La curva de infectados crece mucho al principio de una epidemia. La mejor estrategia es conseguir que se desacelere su crecimiento, de modo que el pico se retrase en el tiempo y se mantenga lo más bajo posible para evitar el colapso del sistema de salud. Este aplanamiento de la curva se logra al bajar la tasa de transmisión. Hemos visto que eso es posible si se baja la cantidad de contactos que cada uno tiene, y se toman otras medidas como la higiene estricta mediante el lavado de manos, el uso de barbijos y el distanciamiento social. En forma simultánea al aplanamiento de la curva de infectados, comienza a crecer la curva de recuperados. Ambas se van compensando hasta que, más tarde, la curva de infectados, empieza a descender. O sea que, aunque hoy se utilicen otros modelos mucho más sofisticados, el comportamiento de la población de infectados será similar al que se muestra con el modelo SIR, en la FIGURA 2. 

A partir de la realización de ensayos con los modelos matemáticos (simulaciones computacionales), que incluyen diferentes valores de los parámetros tales como la tasa de transmisión, puede decirse que la evolución de la pandemia en Argentina depende fundamentalmente de nosotros. Y que se debe tener en cuenta que hay situaciones epidemiológicas locales muy diferentes de las globales. 

Es posible concluir que el gran desafío que tenemos por delante es lograr que la curva de infectados no se dispare lo cual significa, en otras palabras, que debemos conseguir que el tiempo de duplicación de los casos infectados no disminuya. 

* Dra. en Matemática. Prof. de la Facultad de Ingeniría de la UNLP.