Matemáticas y pandemia: ¿Qué significa "achatar" la curva de infectados?

Por Leandro Andrini | Investigador (CONICET)

Desde hace semanas escuchamos hablar de “crecimiento exponencial” y de “achatar la curva”. La primera de las frases pertenece a un vocabulario al que estamos casi acostumbrados, porque independientemente el crecimiento que se haya registrado en cualquier área se atribuye como exponencial (sea o no sea así tal crecimiento). La segunda la estamos aprendiendo a fuerza de quedarnos en casa en la cuarentena. Se nos dice que debemos permanecer en nuestros domicilios para “planchar la curva”.

Para hablar de “achatar la curva” antes tenemos que hablar de “crecimiento exponencial”.

Vamos a suponer que nuestro sistema de contar es “un día” (contamos en días), el caso más sencillo de crecimiento exponencial es el de la duplicación de lo que teníamos el día anterior. Esto es, si el primer día tenemos 1, el segundo día vamos a tener 2, el tercer día vamos a tener 4, el cuarto día 8, el quinto 16, y así siguiendo… en general esto suele representarse en diagramas o gráficos. Abajo, inmediatamente, tres representaciones de esta situación: la (a) que es un esquema de línea, la (b) un esquema de árbol, y la (c) un gráfico de puntos de datos con su respectivo ajuste de datos y al lado un gráfico de barras (son las dos maneras más usadas para informar este tipo de datos).

(a) Esquema de línea.

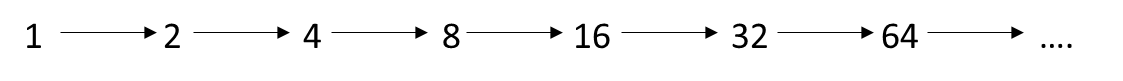
(b) Esquema de árbol.

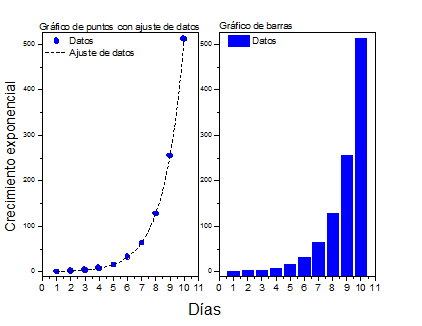
Sugerencia: se puede “jugar” haciendo esquemas de línea, y/o esquemas de árbol, suponiendo, por ejemplo, que se triplica (cuadriplica, etc.) lo que se tenía el día anterior. Ahí se vuelve notorio lo que se llama “control de conteo”, que en la jerga que se ha impuesto se denomina “achatar la curva” (o “planchar la curva”).

En el gráfico de puntos con ajuste de datos (d) vemos esto de “achatar la curva”.

(d) Gráfico de crecimiento exponencial con ajuste de datos

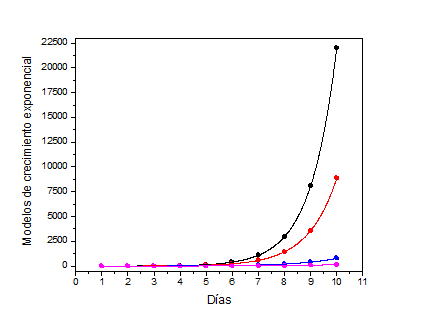
En todos los casos se trata de crecimientos exponenciales. Vemos que el representado con color negro, en un mismo intervalo de tiempo, es el que alcanza el mayor valor, mientras que el rosa es el que tiene los valores más bajos. En tanto que los representados por colores rojo y azul representan valores intermedios. Acá vemos, gráficamente, el significado de “achatar la curva”, es decir, controlar el número de contagios (para el caso del COVID-19) por día, de manera de controlar el crecimiento de la curva.

¿De qué depende ese “achatar la curva”? En toda epidemia, depende de muchos factores: de cuán contagioso es el virus, de cuantos contactos tiene cada infectado (aquí entra en juego el “quedarse en casa”), de cuantos “vectores” puede tener el virus (sólo transmitido por humanos, transmitido humanos e insectos, etc.).

¿Por qué las curvas son exponenciales? Eso es motivo para otra conversación…

PS: Aclaración necesaria: en todos los casos se trabajó con datos modelos, no representa progresión de la infección de COVID-19 en ningún lado (sólo para hacer ilustrativa la situación).

* Investigador (CONICET) en Área Química (Química-Física). Responsable de la sección Ciencia y Tecnología AGENCIA PACO URONDO.